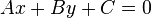ORIGEN E HISTORIA DE LA GEOMETRÍA
"Antes del pensamiento que aspira a una coherencia lógica
hallamos fe en una u otra magia".
hallamos fe en una u otra magia".
Geometría antes de los griegos
El origen de la Geometría coincide con el origen de la humanidad. El pensamiento precientífico apoyado sobre el monoteísmo naturalista de Amenhotep IV funda en el siglo XIV aC culto a la nueva imagen del dios Ra representado con un círculo dorado. La abstracción del pensamiento mágico representa el primer acercamiento -informal e intuitivo- a la Geometría. Anteriormente, en el siglo XXVII a.C., el emperador chino Hoang-Ti mandó construir un observatorio astronómico con el fin principal de corregir el calendario.Las primeras civilizaciones mediterráneas adquieren poco a poco conocimientos geométricos de carácter muy práctico basados en fórmulas -mejor dicho, algoritmos expresados en forma de recetario-, para calcular áreas y longitudes. La finalidad era práctica al pretender con ello calcular la producción proporcional de las parcelas de tierra para determinar los impuestos, o reconstruir las parcelas de tierra después de las inundaciones. El conocimiento geométrico tanto de egipcios como de las culturas mesopotámicas pasa íntegramente a la cultura griega a través de Tales de Mileto, la secta de los pitagóricos, y esencialmente de Euclides.
La Geometría antes de Euclides
Tales visita Egipto una larga temporada y aprende de los sacerdotes y escribas egipcios lo referente a sus conocimientos en general. Impresiona ahora -tanto como a los egipcios- que fuera capaz de razonar y medir entonces la altura de la pirámide de Keops y de predecir un eclipse solar con asombrosa precisión.
La Geometría griega es la primera en ser formal. Parte de los conocimientos concretos y prácticos de las civilizaciones egipcia y mesopotámicas, y da un paso de abstracción al considerar los objetos como entes ideales -un cuadrado cualquiera, en lugar de una pared cuadrada concreta, un círculo en lugar del ojo de un pozo...- que pueden ser manipulados mentalmente, con la sola ayuda de la regla y el compás. Aparece por primera vez la demostración como justificación de la veracidad de un conocimiento, aunque en un primer momento fueran más justificaciones intuitivas que verdaderas demostraciones formales.
La figura de Pitágoras y de la secta de seguidores pitagóricos tiene un papel central, pues eleva a la categoría de elemento primigenio el concepto de número, arrastrando a la Geometría al centro de su doctrina -en este momento inicial de la historia de la Matemática aún no existe distinción clara entre Geometría y Aritmética-, y asienta definitivamente el concepto de demostración formal como única vía de establecimiento de la verdad en Geometría.
Esta actitud permitió la medición de la tierra por Eratóstenes, así como la medición de la distancia a la luna, y la invención de la palanca por Arquímedes, varios siglos después.
En el seno de los pitagóricos surge la primera crisis de la Matemática: la aparición de los inconmensurables aunque esta crisis es de carácter más filosófico y aritmético que geométrico.
Surge entonces un problema a nivel lógico: una demostración parte de una o varias hipótesis para obtener una tesis. La veracidad de la tesis dependerá de la validez del razonamiento con el que se ha extraído (esto será estudiado por Aristóteles al crear la Lógica) y de la veracidad de las hipótesis. Pero entonces debemos partir de hipótesis ciertas para poder afirmar con rotundidad la tesis. Para poder determinar la veracidad de las hipótesis, habrá que considerar cada una como tesis de otro razonamiento, cuyas hipótesis deberemos también comprobar. Se entra aparentemente en un proceso sin fin en el que, indefinidamente, las hipótesis se convierten en tesis a probar.
Euclides y los Elementos
Vinculado al Museo de Alejandría y a su Biblioteca, Euclides zanja la cuestión al proponer un sistema de estudio en el que se da por sentado la veracidad de ciertas proposiciones por ser intuitivamente claras, y deducir de ellas todos los demás resultados. Su sistema se sintetiza en su obra cumbre los Elementos, modelo de sistema axiomático-deductivo. Sobre tan sólo cinco postulados y las definiciones que precisa construye toda la Geometría y la Aritmética conocidas hasta el momento. Su obra, en XIII volúmenes, perdura como única verdad geométrica hasta el siglo XIX.
Entre los postulados en los que Euclides se apoya hay uno (el quinto postulado) que trae problemas desde el principio. Su veracidad está fuera de toda duda, pero tal y como aparece expresado en la obra, muchos consideran que seguramente puede deducirse del resto de postulados. Durante los siguientes siglos, uno de los principales problemas de la Geometría será determinar si el V postulado es o no independiente de los otros 4, es decir, si es necesario considerarlo como un postulado o es un teorema, es decir, puede deducirse de los otros, y por lo tanto colocarse entre el resto de resultados de la obra.
Después de Euclides
Euclides cierra la etapa de Geometría griega -a excepción de Pappus en el 350 aC-, y por extensión la etapa del mundo antiguo y medieval-, a excepción también de las figuras de Arquímedes y Apolonio.
Arquímedes estudió ampliamente las secciones cónicas, introduciendo en la Geometría las primeras curvas que no eran ni rectas ni circunferencias, aparte de su famoso cálculo del volumen de la esfera, basado en los del cilindro y el cono.
Apolonio trabajó en varias construcciones de tangencias entre círculos, así como en secciones cónicas y otras curvas.
Los tres problemas de la Antigüedad
La Geometría griega es incapaz de resolver tres famosos problemas que heredarán los matemáticos posteriores. Los tres problemas debían ser resueltos entonces utilizando regla y compás, únicos instrumentos aceptados en la Geometría de Euclides. Añadido a estos tres problemas, la demostración de si el V postulado es o no es un teorema deducible de los cuatro anteriores se considera además de otro problema clásico de la Geometría helenística el hilo conductor hasta las Geometrías No Euclidianas del siglo XIX. Los tres otros problemas son:
La duplicación el cubo
Pericles muere de la terrible peste que asola Atenas.Cuenta la leyenda que una terrible peste asolaba la ciudad de Atenas, hasta el punto de llevar a la muerte a Pericles. Una embajada de la ciudad fue al oráculo de Delos, consagrado a Apolo (en ciertas fuentes aparece el oráculo de Delfos, en lugar del de Delos, también consagrado a Apolo), para consultar qué se debía hacer para erradicar la mortal enfermedad. Tras consultar al Oráculo, la respuesta fue que se debía duplicar el altar consagrado a Apolo en la isla de Delos. El altar tenía una peculiaridad: su forma cúbica. Prontamente, los atenienses construyeron un altar cúbico cuyos lados eran el doble de las del altar de Delos, pero la peste no cesó, se volvió más mortífera. Consultado de nuevo, el oráculo advirtió a los atenienses que el altar no era el doble de grande, sino 8 veces mayor, puesto que el volumen del cubo es el cubo de su lado ((2l)3 = 23l3 = 8l3). Nadie supo cómo construir un cubo cuyo volumen fuese exactamente el doble del volumen de otro cubo dado, y el problema matemático persistió durante siglos (no así la enfermedad).
La trisección del ángulo
Este problema consiste en dividir un ángulo cualquiera en tres ángulos iguales, empleando únicamente la regla y el compás, de manera que la suma de las medidas de los nuevos tres ángulos sea exactamente la medida del primero. Dadas las condiciones nadie ha logrado hacerlo.
La cuadratura del círculo
La cuadratura del círculo consiste en tratar de obtener, dado un círculo, un cuadrado cuya área mide exactamente lo mismo que el área del círculo. Anaxágoras fue el primero en intentar resolverlo, dibujando en las paredes de su celda cuando fue hecho prisionero por explicar diversos fenómenos que los griegos atribuían a los dioses. Tampoco pudo ser resuelto por los geómetras de la antigüedad, y llegó a ser el paradigma de lo imposible. Como curiosidad, el filósofo inglés David Hume llegó a escribir un libro con supuestos métodos para resolver el problema. Hume no tenía conocimientos matemáticos serios, y nunca aceptó que todos sus métodos fallaban.
La Geometría en la Edad Media
Durante los siguientes siglos la Matemática comienza nuevos caminos - Álgebra y Trigonometría - de la mano de indios y árabes, y la Geometría apenas tiene nuevas aportaciones, excepto algunos teoremas de carácter más bien anecdótico. En Occidente, a pesar de que la Geometría es una de las siete Artes Liberales (encuadrada concretamente en el Quadrivium), las escuelas y universidades se limitan a enseñar los Elementos, y no hay aportaciones, excepto tal vez en la investigación sobre la disputa del V postulado. Si bien no se llegó a dilucidar en este periodo si era o no independiente de los otros cuatro, sí se llegaron a dar nuevas formulaciones equivalentes de este postulado.
La Geometría en la Edad Moderna
La Geometría Proyectiva
Es en el Renacimiento cuando las nuevas necesidades de representación del arte y de la técnica empujan a ciertos humanistas a estudiar propiedades geométricas para obtener nuevos instrumentos que les permitan representar la realidad. Aquí se enmarca la figura del matemático y arquitecto Luca Pacioli, de Leonardo da Vinci, de Alberto Durero, de Leone Battista Alberti, de Piero della Francesca, por citar sólo algunos. Todos ellos, al descubrir la perspectiva y la sección crean la necesidad de sentar las bases formales en la que se asiente las nuevas formas de Geometría que ésta implica: la Geometría proyectiva, cuyos principios fundamentales aparecen de la mano de Desargues en el siglo XVII. Esta nueva geometría de Desargues fue estudiada ampliamante ya por Pascal o por de la Hire, pero debido al interés suscitado por la Geometría Cartesiana y sus métodos, no alcanzó tanta difusión como merecía hasta la llegada a principios del siglo XIX de Gaspard Monge en primer lugar y sobre todo de Poncelet.
La Geometría Cartesiana
La aparición de la Geometría Cartesiana marca la Geometría en la Edad Moderna. Descartes propone un nuevo método de resolver problemas geométricos, y por extensión, de investigar en Geometría.
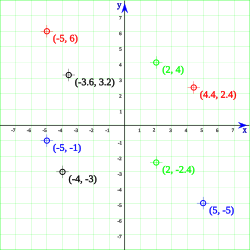
El nuevo método se basa en la siguiente construcción: en un plano se trazan dos rectas perpendiculares (ejes) -que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical-, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado (x,y), siendo x la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e y la distancia al otro eje (al horizontal).
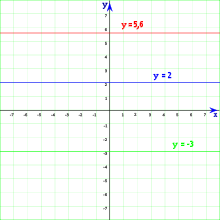
En la coordenada x, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje vertical (eje de ordenadas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada y, el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje horizontal (eje de abscisas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso). A la coordenada x se la suele denominar abscisa del punto, mientras que a la y se la denomina ordenada del punto.
Existe una cierta controversia aun hoy sobre la verdadera paternidad de este método. Lo único cierto es que se publica por primera vez como Geometría Analítica, apéndice al Discurso del Método, de Descartes, si bien se sabe que Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes. Aunque Omar Khayyam ya en el siglo XI utilizara un método muy parecido para determinar ciertas intersecciones entre curvas, es imposible que alguno de los citados matemáticos franceses tuviera acceso a su obra.
Lo novedoso de la Geometría Analítica (como también se conoce a este método) es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: 2x + 6y = 0) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia x2 + y2 = 4, la hipérbola xy = 1 ). Esto convertía toda la Geometría griega en el estudio de las relaciones que existen entre polinomios de grados 1 y 2. Desde un punto de vista formal (aunque ellos aun lo sabían), los geómetras de esta época han encontrado una relación fundamental entre la estructura lógica que usaban los geómetras griegos (el plano, la regla, el compás...) y la estructura algebraica del ideal formado por los polinomios de grados 0, 1 y 2 del Anillo de polinomios \mathbb{R}[x,y], resultando que ambas estructuras son equivalentes. Este hecho fundamental -no visto con nitidez hasta el desarrollo del Álgebra Moderna y de la Lógica Matemática entre finales del siglo XIX y principios del siglo XX-, resulta fundamental para entender por qué la Geometría de los griegos puede desprenderse de sus axiomas y estudiarse directamente usando la axiomática de Zermelo-Fraenkel, como el resto de la Matemática.
El método original de Descartes no es exactamente el que se acaba de explicar. Descartes utiliza solamente el eje de abscisas, calculando el valor de la segunda componente del punto (x,y) mediante la ecuación de la curva, dándole valores a la magnitud x. Por otro lado, Descartes sólo considera valores positivos de las cantidades x e y, dado que en la época aun resultaban "sospechosos" los números negativos. Como consecuencia, en sus estudios existen ciertas anomalías y aparecen curvas sesgadas. Con el tiempo se aceptaron las modificaciones que muestran el método tal y como lo conocemos hoy en día.
Los nuevos métodos
Agotamiento del método sintético
La aparición de la Geometría Analítica trae consigo una nueva forma de entender la Geometría. El nuevo método, algebraico, sustituye al antiguo, el sintético, consistente en establecer unos axiomas y unas definiciones y deducir de ellos los teoremas. El método sintético está a estas alturas casi agotado (aunque aun dará algunos resultados interesantes, como la característica de Euler, la naturaleza de estos resultados no es ya tanto geométrica como topológica, y los resultados realmente importantes que se hagan en adelante en el campo de la Geometría ya vendrán de la mano de métodos algebraicos o diferenciales), da paso al método algebraico: estudio de los objetos geométricos como representaciones en el espacio de ciertas ecuaciones polinómicas, o dicho de otro modo, del conjunto de raíces de polinomios. El método sintético sólo volverá a abordarse cuando aparezcan las geometrías no euclídeas, y definitivamente deja de ser un instrumento de investigación geométrica a principios del siglo XX, quedando relegado a un conjunto de instrumentos y herramientas para la resolución de problemas, pero ya como una disciplina cerrada.
Los límites del método algebraico
El método algebraico se ve posibilitado por un avance en Álgebra hecho durante el siglo XVI, la resolución de las ecuaciones de grado 3º y 4º. Esto permite generalizar la Geometría, al estudiar curvas que no son dadas por polinomios de segundo grado, y que no pueden construirse con regla y compás -además de las cónicas, excluyendo a la circunferencia, claro-. Pero este método, que terminará constituyendo una disciplina propia, la Geometría Algebraica, tardará aun mucho -siglo XX- en salir de unas pocas nociones iniciales, prácticamente inalteradas desde Descartes, Fermat y Newton. La razón será la imposibilidad de resolver por radicales la ecuación de quinto grado, hecho no descubierto hasta el siglo XIX, y el desarrollo de la Teoría de Anillos y del Álgebra Conmutativa.
El Cálculo Infinitesimal
El método algebraico tiene otra generalización natural, que es la de considerar una curva no solo como una ecuación polinómica, sino como una ecuación f(x,y) = 0 en la que el polinomio es ahora sustituido por una función cualquiera f. La generalización de todo esto desde el plano (2 coordenadas) al estereoespacio (3 coordenadas) se hace de forma natural añadiendo un tercer eje perpendicular (eje z) a los dos ya considerados, y las funciones tomarán la forma f(x,y,z).
Ya Isaac Barrow descubre gracias a la Geometría Analítica la relación entre la tangente a una curva y el área que encierra entre dos puntos y los ejes coordenados en su famosa Regla de Barrow, antes incluso de que Newton y Leibnitz dieran cada uno su exposición del Cálculo Infinitesimal. La relación entre el Análisis Matemático y la Geometría es así estrechísima desde incluso los orígenes de aquél. Las ideas geométricas no sólo fueron la base de los instrumentos iniciales del Cálculo Infinitesimal, sino que fueron en gran medida su inspiración. Por eso resulta natural que en un primer momento, Descartes, Newton o los Bernoulli no distinguieran entre los conceptos de curva y de función de una variable (o si se quiere, de curva y los ceros de una función de dos variables). Fue Euler el primero en empezar a intuir la diferencia, y el primero también en ampliar este tipo de estudios a las superficies (como función de dos variables o como el conjunto de los ceros de una función de tres variables). El trabajo de Monge continúa por esta línea.
En adelante, y hasta la aparición de Gauss, la Geometría queda supeditada a sus aplicaciones en Mecánica y otras ramas de la Física por medio de la resolución de Ecuaciones Diferenciales. Se estudia en especial la interpretación geométrica de las ecuaciones diferenciales (tanto de la solución en sí como problemas asociados a ellas, como puede ser el de las curvas ortogonales). En esta época aparece el que será el caballo de batalla de la Geometría Diferencial: el Teorema de la Función Implícita.
Fue Huygens el primero en estudiar la curvatura de una curva plana, aunque parece que fue Clairaut el que usa con maestría y fija el concepto.
La Geometría en la Edad Contemporánea
Gauss devuelve el carácter geométrico que impregna parte del Análisis Matemático, fundamentalmente con dos contribuciones: el nacimiento de la Variable Compleja y de la Geometría Diferencial.
Pero no son las únicas contribuciones de éste genio al campo de la Geometría. En su adolescencia se vio dividido entre dedicarse a la Filología o a la Matemática. A los 17 descubrió la manera de construir el polígono regular de 17 lados, y la condición necesaria y suficiente para que un polígono regular pueda construirse. Esto determinó su vocación.
En su primera demostración del Teorema Fundamental del Álgebra (de las cinco que realizó a lo largo de su carrera) sentó las bases del Análisis de Variable Compleja, usando la interpretación geométrica de los números complejos como vectores fijos del plano (no en este lenguaje, que será introducido mucho más tarde). Por cierto, se atribuye a Gauss la paternidad de esta idea. Primero Wessel y luego Argand se le anticiparon, pero nadie conocía los estudios de ambos. Aunque no es propiamente obra suya, pues la Variable Compleja está desarrollada fundamentalmente por Cauchy, sí es el primero en abordarla seriamente, y sobre todo le da una interpretación geométrica que marcará el desarrollo de esta rama.
Pero la principal contribución de Gauss a la Geometría es la creación de la Geometría Diferencial, retomando las ideas que sobre las relaciones entre el Análisis Matemático y la Geometría había hasta entonces y desarrollándolas ampliamente.
Partiendo de la base de que la Geometría estudia el espacio, las curvas y las superficies, establece la noción fundamental de curvatura de una superficie. Gracias a ella, y a la definición de geodésica, demuestra que si consideramos que una geodésica es una curva con menor distancia entre dos puntos sobre una superficie (es decir, si tenemos dos puntos sobre una superficie, el camino más corto entre esos dos puntos sin salirnos de la superficie es un segmento de geodésica), concepto totalmente análogo sobre la superficie al de recta en el plano, existen superficies en las que los triángulos formados por las geodésicas miden más de la medida de dos ángulos rectos, y otras en las que mide menos. Esto, esencialmente, es contradecir el V postulado de Euclides.
Estas consideraciones llevaron a Gauss a considerar la posibilidad de crear geometrías no euclídeas, pero aunque a esas alturas ya era el matemático más prestigioso de Europa, consideró que la mentalidad de la época no estaba preparada para un resultado de tal magnitud, y nunca publicó esos resultados. Sólo vieron la luz cuando Bolyai publicó su geometría no euclídea, y comprobó que la comunidad científica general aceptaba el resultado.
Así que, por un lado, Gauss fue el primero en crear una geometría no euclídea, y por otro fue el creador de la Geometría Diferencial y precursor de la Variable Compleja.
Además, Gauss es el primero en considerar una nueva propiedad en la Geometría: la orientación.